11.5.2.5 write a pseudo-code of binary search for the solution of a specific problem 

Search in an array

How to find key value in an array?

We can apply searching in an array.

Searching is looking through the elements of an array to see if a particular piece of data is there.

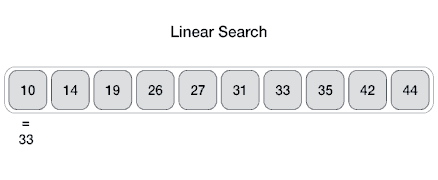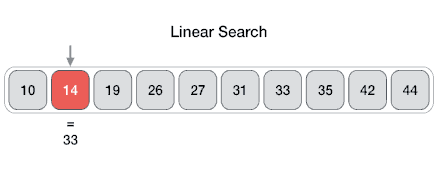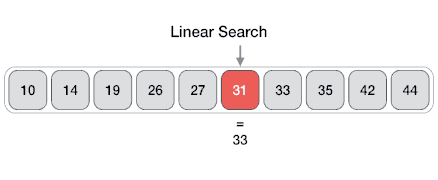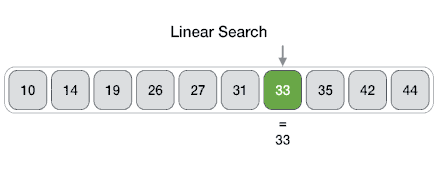
Linear search

Linear search is a simple algorithm. It is carried out by comparing the array of elements to match the key value.

Pseudocode of linear search

key = 33
found = False
FOR i FROM  0 TO array.length - 1
   IF  array[i] = key 
      THEN found = True
   endIF
endFOR
IF found 
   THEN Output "Element is found"
      ELSE Output "Element is not found"

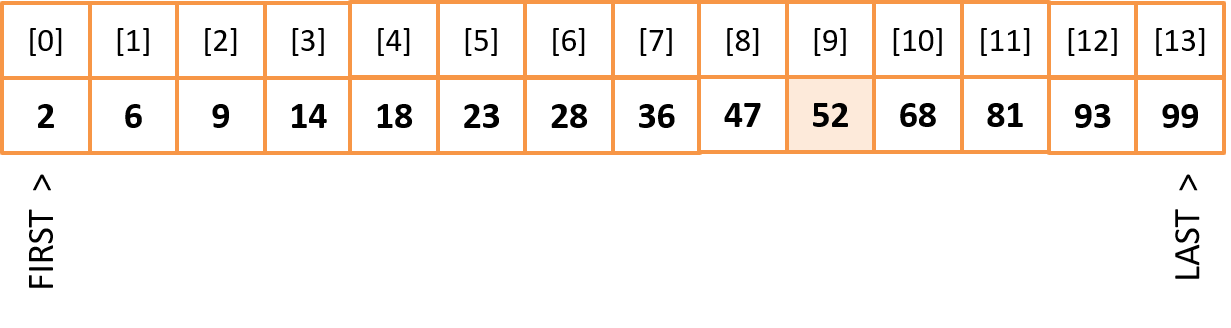
Binary search

Binary search divides the array in half and determines the part of the array that contains the key value. 

To perform a binary search, the array must be sorted. 

Array

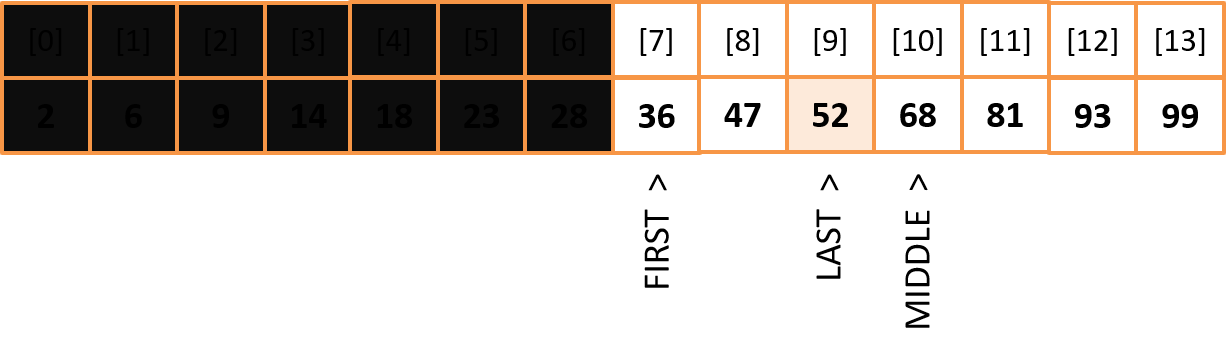
Key value: Target = 52

Define two variables for bounds: FIRST = 0 and LAST = Array.length - 1

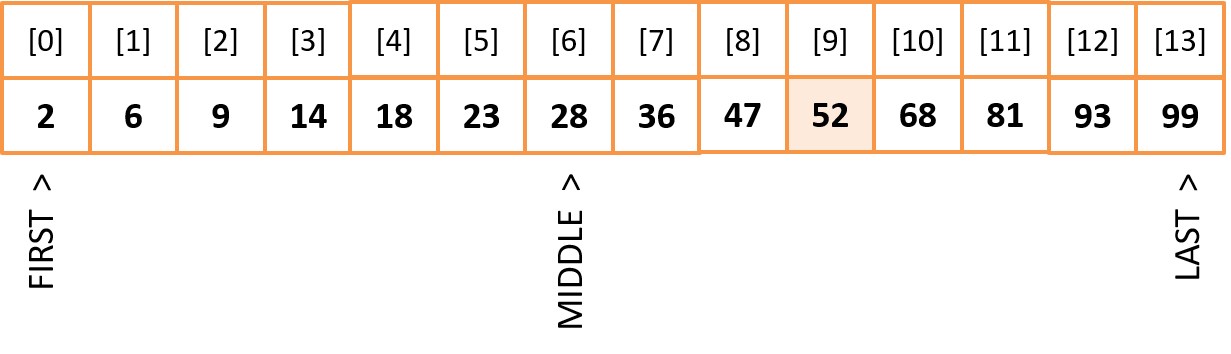
Find MIDDLE item: MIDDLE = (FIRST + LAST) / 2 (integer number)

MIDDLE = (0 + 13) / 2 = 6

The key value is to the right of the middle index, so we move the left bounce.

FIRST = MIDDLE + 1

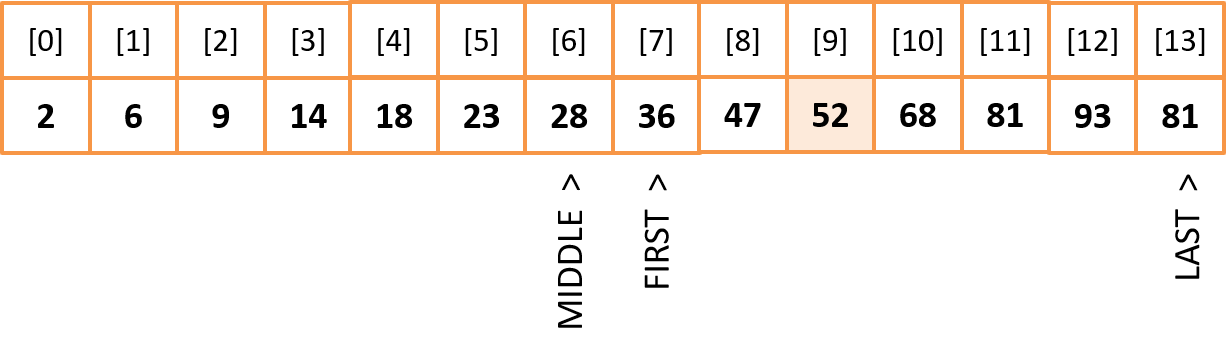
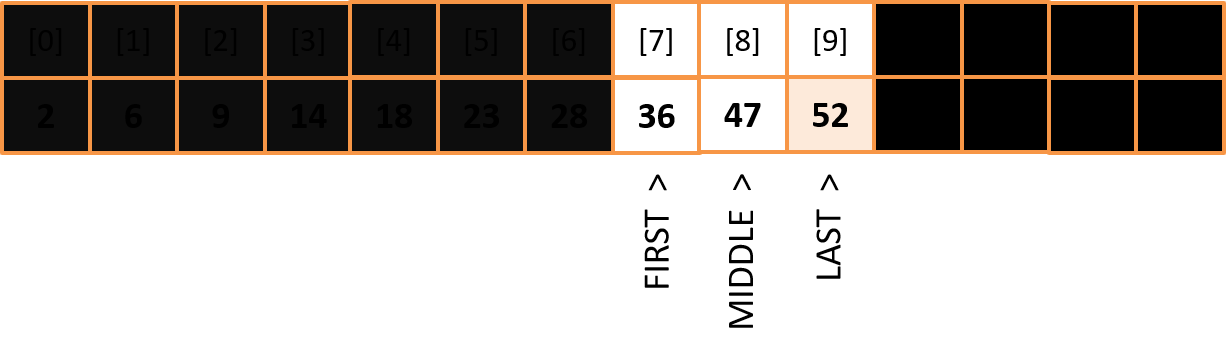
Eliminate the unnecessary part and define MIDDLE: MIDDLE = (7 + 13) / 2 = 10

The key value is to the left of the middle index, so we move the right bounce.

LAST = MIDDLE - 1

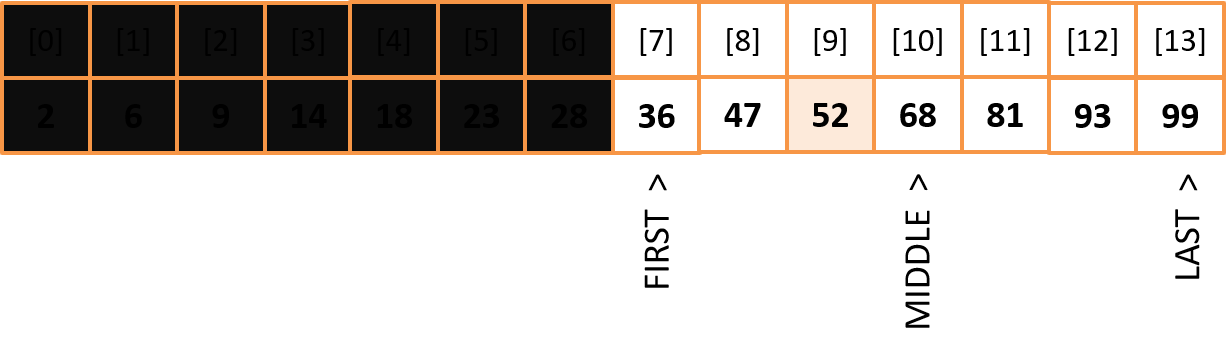
MIDDLE = (7 + 9) / 2 = 8

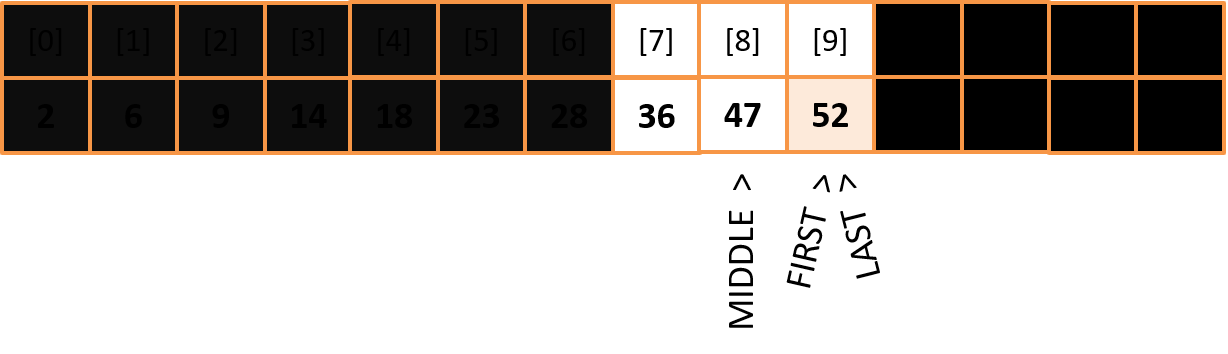
The key value is to the right of the middle index, so we move the left bounce.

FIRST = MIDDLE + 1

MIDDLE = (9 + 9) / 2

Array[MIDDLE] = Target

Search is over

Pseudocode of binary search

Target = 52
FIRST = 0
LAST = ARRAY.length – 1
MIDDLE = (FIRST + LAST) / 2
FOUND = FALSE
while FIRST <= LAST and FOUND = FALSE
  if ARRAY[MIDDLE] = TARGET then
    FOUND = TRUE
  else if ARRAY[MIDDLE] > TARGET then
    LAST = MIDDLE – 1
  else
    FIRST = MIDDLE + 1
  end if
  MIDDLE = (FIRST + LAST) / 2
end while
if FOUND = TRUE
  Output MIDDLE or Output "Target is found"
else
  Output "Target is not found" 
end if 

What is the maximum number of search steps required for n items?

2ⁿ > size of array, where n = max searches

For example, 

for 70 items max searches = 7, because 2⁶<70, 2⁷>70

Activity:

Searching algorithm

Questions:

Exercises:

Ex. 1

Quiz "Binary search"

Ex. 2 Define max searches for N-ordered elements

Ex. 3 Arrange Binary search lines in order

Ex. 4 Binary search (Author: Litvinova Olga CS teacher of NIS Pavlodar)

Ex. 5 Write a program to implement binary search

1) Target = 52

2) Fill array of 100 random numbers

3) Sort Array

4) Output array

5) Implement binary search

6) Output index of an item if Target will be found or message "Target is not found"

Ex. 6 Write a program to check random array numbers using binary search.

primes = [79, 83, 2, 5, 7, 11, 13, 89, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 3, 67, 71, 17, 73, 97]

Exam questions: