12.1.1.6 use binary numbers with a fixed point to represent fractional numbers with a given number of bits. 

12.1.1.7 represent positive and negative floating-point decimal numbers in binary. 

Fix point numbers and Floating point numbers

I. Fixed point numbers

Real number - a number with a fractional part.

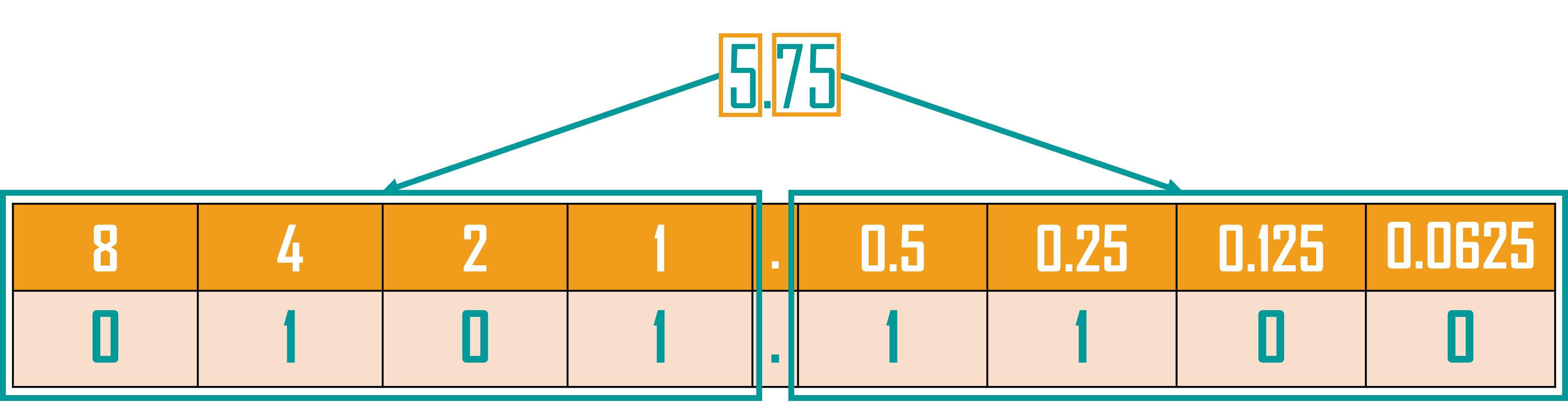
The number 68.25 represents 6 tens, 8 units, 2 tenths, 5 hundredths.

In binary, the equivalent place values are 

128  64  32  16  8  4  2  1  .  1/2  1/4  1/8  1/16

The number 68/25 can be expressed as 68 + 1/4, and using the place values above converts to

Matching binary fractions and decimal fraction

Examples. Using one byte to hold each number, with an imaginary binary point fixed after the fourth digit, convert the following unsigned decimal numbers to binary.

5.75₁₀ = 0101.1100₂

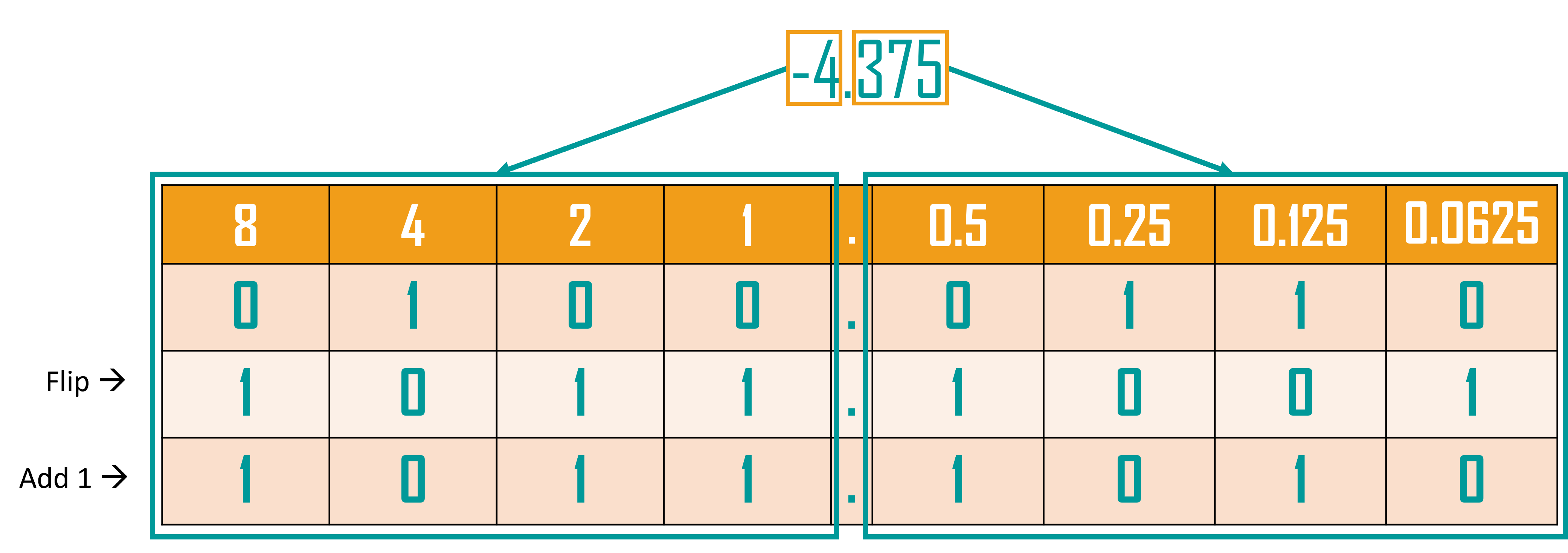
-4.375₁₀ = 1011.1010₂

II. Floating point numbers

Why do we use float point real numbers?

1) a very large number

600 000 000 000 000 = 0.6 х 10¹⁵

2) a very small number

0.000 000 000 03 = 0.3 х 10^-10

Example of a denary floating-point number

Example of a binary floating-point number

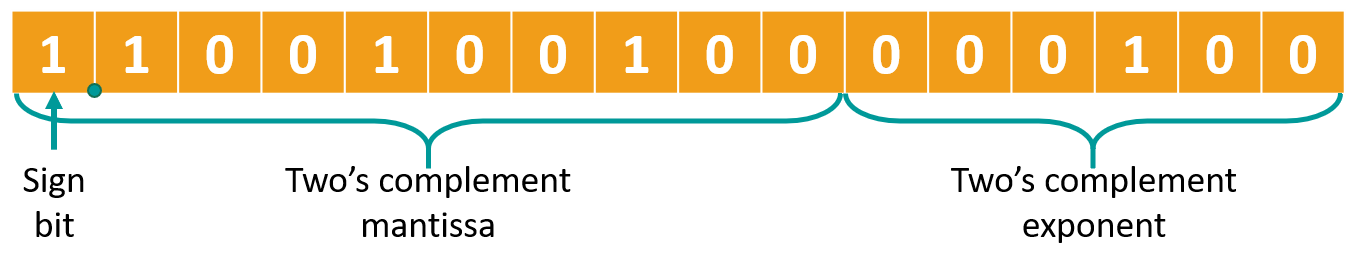
Why use binary floating-point numbers

Fixed-point binary allows computers to represent fractions but has a limited range. Even with 4 bytes (32 bits) and 8 bits for the fractional part, the largest representable number is just over 8 million. This limitation makes it unsuitable for very large numbers.

Floating-point notation overcomes this by using a mantissa (main digits) and an exponent (position of the decimal point), similar to scientific notation in decimal. For example, 0.12 × 10¹⁵ has 0.12 as the mantissa and 10¹⁵ as the exponent.

In binary, two bytes (16 bits) can be divided into 10 bits for the mantissa and 6 bits for the exponent, allowing a much wider range of numbers to be represented efficiently.

Converting binary floating-point to decimal

1) Find the sign of the mantissa (write it down)

2) Write down the mantissa. If the mantissa is negative, convert the two's complement over it.

3) Find the exponent value. If the exponent is negative, convert the two's complement over it.

4) Move the floating point in the mantissa to the distance that defines the exponent (point 3), left for negative exponent, right for positive.

5) Calculate the whole part and the fractional part. Put a sign (point 1)

Calculate the value of the number

Example 1. Mantissa is positive, Exponent is positive

The mantissa m = 0.100100100₂

The exponent e = 000100₂ = 4₁₀

Therefore the value is 0.100100100₂ x 2⁴ = 1001.001₂ = 9.125₁₀

Example 2. Mantissa is negative, Exponent is positive

The mantissa is a negative value. Converting the two's complement gives m = - 0.011011100₂

The exponent e = 000100₂ = 4₁₀

Therefore the value is - 0.011011100₂ x 2⁴ = - 110.111₂ = - 6.875₁₀

Example 3. Mantissa is positive, Exponent is negative

The mantissa is  m = 0.101000000₂

The exponent is a negative value. Converting the two's complement gives e = - 000010₂ = - 2₁₀

Therefore the value is 0.101₂ x 2^-2 = 0.00101₂ = 0.15625₁₀

Example 4. Mantissa is negative, Exponent is negative

The mantissa is a negative value. Converting the two's complement gives  m = - 0.101000000₂

The exponent is a negative value. Converting the two's complement gives e = - 000010₂ = - 2₁₀

Therefore the value is - 0.101₂ x 2^-2 = 0.00101₂ = - 0.15625₁₀

Floating Point Binary Converter

Normalisation float point numbers

• The normalised version of a positive fractional number has no leading zeros after the binary point — a normalised positive number always starts as 0.1;

• The normalised version of a negative fractional number has no leading ones after the binary point — a normalised negative number always starts as 1.0.

Questions:

Exercises:

Ex. 1

Ex. 2

Ex. 3

Exam questions: